因数分解と詰将棋

将棋と数学って共通点が多くあります。

将棋には「詰将棋」というものがあります。

ここではルールの説明をしていると大変なことになってしまうので、

ある程度わかっている前提で話をします。

全然わからない人は、この記事はスルーしてください。

詰将棋と数学の図形問題は共通点が多いことは、

ある程度すぐにわかることだと思います。

なので、ここでは因数分解だって共通点があるよってことを

話してみようかなって思います。

聞いてみようかなって思った人だけ続きをどうぞ！

これは、簡単な３手詰めの問題です。

（これくらいは私もすぐ作れます（笑））

初手「２二金」が見つけられるかどうかだけですが、

一瞬でわかる人は、「同玉」に「３二飛成」が詰みの形

だとわかる人です。

この問題自体に紛れる要素はほとんどないので、

遅い人でも見つけられると思いますが、

指した後の先が見えることがポイントになります。

言いたいことは、そのことです。

これ、関連記事です

では、数学の因数分解ですが、

やはり先の形が見えないと次に進めることができません。

例えばこの問題ですが、これは４つの項の組み合わせ方がポイントです。

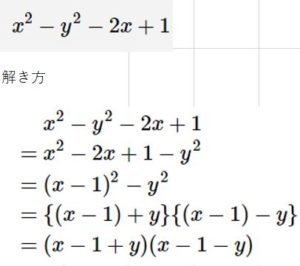
Xの2乗と‐２Xと＋１で（X－１）の２乗になることがわかれば

答えまでいけるのですが、それに気づかない人はたどり着けません。

つまり、詰将棋があまりできない人や因数分解があまり得意でない人は、

その先のイメージがわかないのですね。

では、どうしたらいいのでしょうか。

………

それは、やはり量をこなしたり繰り返し行うことで慣れていくことです。

感覚的にサッとひらめくようになるには、経験を積み重ねることです。

そこを怠っていると、いつまでもできなかったり自信のない状態になりますので、

そのことをよくわかってほしいと思います。

今回は、勉強内容はいろいろなことにヒントがあるし、

それをやることで勉強に活かされもするってことを伝えてみました。

ということは、逆に今やっている勉強が、直接的にではなくても

その過程が生きていくうえでのいろいろなことにつながっていく

ということでもあるわけです。

そう考えると、自分に役立つことを学んでいるわけですから、

こう考えると少しは積極的に勉強ができるのではないでしょうか。

少しでもほんとになれば幸いです。